Three Dog Star Night (Part 4)

Welcome back to our discussion on the Drake Equation and the Fermi Paradox! If you haven’t read part 1, part 2, and part 3 already, then it goes without saying that you should start there! This time we’ll be discussing the last factor in the Drake Equation, run some calculations, and conclude by discussing just what sort of an equation it actually is.

Before we dive in, we need to do some brief dimensional analysis. Looking at the factors we’ve discussed thus far, we have four which are purely unitless fractions between zero and one (f_p, f_l, f_i, and f_c), one with units of stars per year (R_*), and one with units of planets per star (n_e). What we’re trying to find (N) has units of planets. If we ignore the values for a moment and look only at the units on each side, we have:

The unit of ‘stars’ cancel out in the usual way fractions do and we are left with:

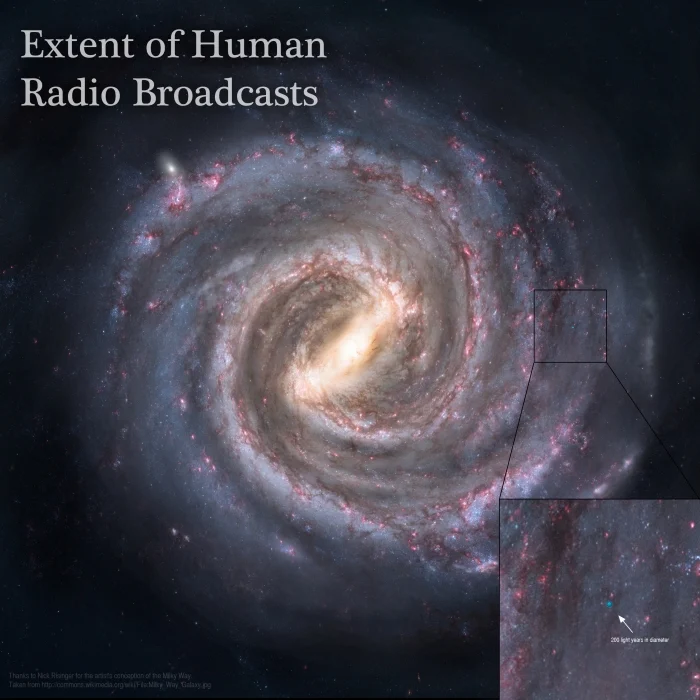
The unitless numbers simply define what type of planet we are talking about. In this case, those are planets which harbor intelligent (f_i), communicating (f_c) life (f_l). We need the units on each side to match for the equal sign to hold true, meaning we need to introduce a final factor with units of years. Since the Drake Equation is all about detecting alien communications, we should only consider how long they actually spend communicating. We could visualize our own radio signals as a ‘bubble’, expanding out from Earth at the speed of light; any civilizations living inside that bubble could theoretically detect us, but for those outside it would be physically impossible as our signals haven’t reached them yet. The longer we broadcast, the bigger the bubble grows, and the number of civilizations that could detect us increases. If instead they are the broadcasters and we are the detectors, the same logic still applies. The longer an alien civilization broadcasts, the better chance we have of detecting them.

_{~100 years of radio visualized on a galactic scale…}

Average Length of Time that a Civilization Broadcasts, L

Like so many of the other factors, this one also has a high degree of uncertainty. It could very well range anywhere between one and one billion centuries. In order to decide which one to use, we need to first examine the reasons why a civilization might stop broadcasting.

The first and most obvious reason is extinction. When the Drake Equation was penned at the height of the Cold War, this was the most widely-assumed reason for the apparent silence of the heavens. With the specter of nuclear war constantly looming overhead, most people simply took it for granted that we would eventually bomb ourselves into oblivion before the end of the 20^th century. Carl Sagan himself assumed this parameter of the Drake Equation was the Great Filter. As a result, he dedicated the rest of his life to warning against the dangers of existential threats like climate change and nuclear war. Then, in 1991, the USSR collapsed, effectively ending the Cold War and drastically reducing the threat of atomic annihilation. There may be a lot we don’t know about the universe, but perhaps the fact that I’m even alive right now to write this article speaks to how little we know about ourselves.

The second reason a civilization may stop broadcasting is that they develop new and better communications technologies. While light is great for the sheer speed at which it travels, it’s also prone to getting scattered, refracted, reflected, diffracted, and absorbed by matter. These reductions in the intensity of a signal are collectively known as ‘attenuation’. Our own atmosphere interferes with numerous wavelengths of light in various ways. Scattering makes the sun and sky appear yellow and blue (the sun looks purely white from space!); absorption of infrared light by CO₂ molecules drives the Earth’s greenhouse effect, and refraction causes the sun to appear to melt into the ocean at sunset. While most of space is indeed pretty empty, giant molecular clouds of gas and dust are common in the arms of spiral galaxies like our own. These structures effectively form walls that are opaque to large swaths of the electromagnetic spectrum. One possible alternative that avoids many of these problems would be communicating through gravitational waves. These ripples in the fabric of spacetime also travel at the speed of light but do not suffer from attenuation the way light waves do. However, we detected the first gravitational wave a mere 6 years ago, so the field of gravitational wave astronomy is still in its infancy. We currently require several kilometers of equipment per detector, with three detectors spread widely across Earth’s surface. It’s going to take a while to refine our detection methods, let alone commercialize it. Although, for a potential alien civilization that reached our technological level 1000 years ago, it may well be within the realm of possibility.

The speed of light is blazingly fast by our standards, but it’s painfully slow when it comes to traversing the enormous distances of interstellar space. Even a message broadcast to the closest star system would take more than four years to arrive. Any reply would then take another four years to get back to us, which makes for a whopping eight year response time for every single message. Unfortunately, nothing can travel through space faster than light, but who says it must be sent through our space? The concept of ‘subspace’ messages is popular in science fiction for a variety of reasons, not the least of which is its convenience as a plot device. The tense disagreements between Picard and the Starfleet high command would lose virtually all of their dramatic effect if it took a millennium to send out a formal reprimand. If we instead had a smaller ‘sub’ space (variously referred to in sci-fi as ‘hyper space’, ‘slip space’, etc.) connecting two distant points in our own universe, we could send and receive messages at the rate we’ve grown accustomed to on Earth. Another similar idea is that of a wormhole. An alien civilization using a network of traversable wormholes for space travel could just as easily use it for two-way communication. Alternatively, if quantum entanglement is found to transmit information, it could also allow for faster-than-light communication. Indeed, wormholes and entanglement may even be the same thing. There are a myriad of reasons to doubt whether using any of these for communication are even physically possible, but the upshot is that if any alien civilizations were using such technology for their interstellar communications, then we would have no chance of detecting them. In principle, we could still detect any transmissions intended to be sent and received on the same planet since radio works perfectly well over short distances. However, such transmissions are generally weaker. Our own TV broadcasts only carry around 100 kilowatts of power, and this dilutes exponentially as distance from the transmitter increases. Despite routine talk about aliens watching our TV reruns, a civilization around Proxima Centauri would need a 2000 foot diameter satellite dish just to receive one photon per frame of The Big Bang Theory. Hardly a worthwhile investment.

_{The REAL reason the aliens will one day destroy Earth}

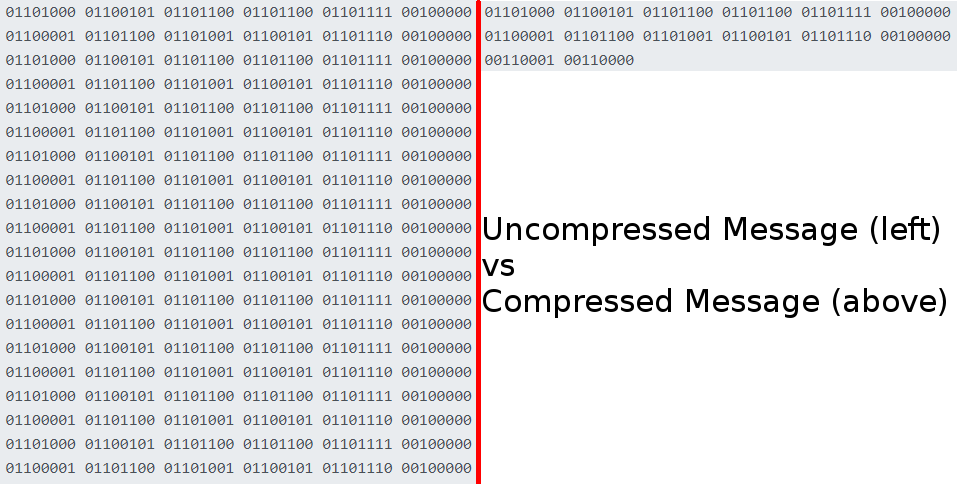
Another assumption in the construction of the Drake Equation was that communication signals would only become more and more noticeable to aliens as technology progressed. Yet rather than making them more and more powerful, we have instead opted to transmit more information per joule. Compression, which removes patterns from signals, is largely responsible for this, but it also makes otherwise easily-recognizable signs of intelligence difficult to differentiate from random background noise. As a simplified example, let’s say we want to broadcast the phrase “hello alien” ten times. We could either broadcast each individual message ten times, or we could broadcast it one time, followed by a number indicating how many times that phrase is repeated. Our message then becomes “hello alien 10”, and we have removed all semblance of repeating patterns from the message. If the intended recipient of our message already knows that a number following a phrase indicates repetition, then no information has been lost, but if they don’t know, then the lack of repeating patterns and the brevity of the transmitted message would make it hard to distinguish from the random noise of the cosmic background. Ultimately, we might not even notice an alien civilization’s broadcasts unless they want us to.

_{If YOU had to pay the bill, the choice here is obvious}

If you’ve ever seen TV static, then you’ve seen some of this cosmic background noise with your own eyes. An estimated 1% of all TV static comes from the Cosmic Microwave Background (CMB), a leftover from when our universe was only 300,000 years old! Other sources of background noise include high energy cosmic rays, which can do some pretty wacky things to our electronics.

Speaking of electronics, another assumption in the Drake Equation is that alien life will be found on habitable planets around stars. This is perfectly reasonable for biological organisms whose chemical processes don’t function well in the cold vacuum of space, but how certain are we that the aliens will be organic? A super-advanced species that goes around wiping others out, so-called cosmic reapers, is a frequently proposed, yet incorrect solution to the Fermi Paradox. Simply replacing one species with another doesn’t solve the problem. After all, the replacements would still be around for us to find, so long as their survival needs, behaviors, and goals are even remotely similar to ours. But what if they aren’t? If we combine these two concepts and consider scenarios in which the replacements are AI, then such machines would have entirely different survival needs and, as a result, entirely different motivations for their behavior. Rather than creating/breaking chemical bonds, they would survive by flipping bits, and the most energy efficient way to flip bits at a given temperature is to do it at the Landauer Limit:

Boltzmann’s Constant (k_B) is a fundamental constant of nature which relates temperature to energy, and ln(2) is equal to approximately 0.693. The only variable that can change in the Landauer Limit is the temperature, and we can easily see from the equation that a lower temperature equates to a lower energy required to flip a single bit. Any AI civilization concerned with maximizing their own survival might logically decide to move their entire civilization into the intergalactic void to increase their longevity through greater computational efficiency. They also might not appreciate organic species using up the universe’s energy for their inefficient biochemical reactions. In short, it’s conceivable that a cybernetic form of the cosmic reapers might exist while simultaneously being exceedingly difficult to detect for anyone not looking in the right place, offering a potential solution to the Fermi Paradox.

_{Coming soon to a planet near you!}

All this is to say that, unfortunately, we can pretty well choose whatever length of time we like for this value of the equation. Those with little faith in humanity, like science writer Michael Shermer, might prefer to set this number to 400 years. I personally tend to be a bit of an optimist about our future and wouldn’t set this number any lower than 10,000. Whichever team you bat for, we can take all of our numbers, multiply them together, and calculate an estimate for the number of intelligent civilizations currently in our galaxy.

For those in the rare Earth, rare intelligence, destined-for-Armageddon camp, we’re probably the only intelligent civilization in the entire Virgo Supercluster:

For the more optimistic among us, the closest E.T.s might only be a few dozen light years away:

Ultimately, our calculation is only as good as our estimates, so should we even spend time discussing an equation like this given how little we know? Have I hoodwinked you all into reading my long diatribes about science by dressing them up with references to pop culture and science fiction?

Well, yes… but actually no.

What IS the Drake Equation?

You see, the Drake Equation isn’t derived from first principles like Newton’s Laws of motion or the Einstein Field Equations, nor was it designed to describe a fundamental aspect of nature. Instead, the Drake Equation is a solution to what’s known as a Fermi Problem. Named after Enrico Fermi, creator of the first nuclear reactor, a Fermi Problem is a type of back-of-the-envelope estimation method designed to approximate answers to extreme scientific calculations. The core idea is surprisingly simple: rather than do the mathematically rigorous calculation to get the precise answer, we can break the problem up into more manageable pieces, throw out some known numbers to place upper/lower bounds on the answer, and finally perform a sanity check at the end. It’s okay to be a bit imprecise with our estimation because any overestimates we make will tend to cancel out with our underestimates. This means that there are actually multiple ways for us to go about making an estimate for the number of other intelligent civilizations in the universe.

_{Aww #$&%, here we go again…}

For example: if every human on Earth formed towers by standing on each other’s heads, how many towers could we make that reach from Earth to the moon? Let’s begin by throwing out some numbers:

• For starters, I know the moon isn’t closer than 100,000 kilometers away, but it also isn’t further than 1,000,000 kilometers away. We’ll split the difference and say the Earth-Moon distance is 500,000 kilometers, and we want one tower per each of these heights.
• I don’t know the average human height. However, I know 5 feet sounds too low, and that 6 ft is too high, so we’ll say instead that it’s 5’ 6”. Converting to metric, that’s about 1.68 meters.
• But wait… adults tend to be taller than children, and most people don’t reach their full height until they’re around 20. I know the average life span is somewhere in the neighborhood of 80, so let’s say that people under the age of 20 represent about 25% of the population and that they have an average height of around 3’. Converted to metric, that’s 0.915 meters.
• I don’t know precisely how many people are on Earth, but I know the number is getting pretty close to 8 billion, so we’ll just say it’s 8 billion.

We’re almost ready to calculate, but first we need to check that our units make sense if we multiply all these numbers together. We know we want our answer to be the number of towers, so:

And indeed, the repeated units on the right side cancel out and leave us with a number of towers! Now, let’s convert our Earth-Moon distance into meters so that it matches the height of each person, i.e. 500,000,000 meters, and we can finally calculate our estimate:

So by this estimate, we could make almost 24 people-tower-of-Babel’s that reached from the Earth to the Moon! Following more rigorous calculations based on physiological data, population estimates, and the Earth-Moon distance that we’ve measured to better than 1 part in 10 billion, we find that we could make a little over 30 such towers. Despite our seemingly terrible estimates, we arrived at a number within 20% of the true value! This general method can be applied to all sorts of seemingly unanswerable questions. Try coming up with and answering some for yourself!

_{Call me, NASA 😉}

In this series of articles about aliens, we’ve discussed topics from astronomy, psychology, chemistry, sociology, history, computer science, mathematics, and theoretical physics, all from a distinctly human perspective. At the end of the day, I guess the Drake Equation is less about analyzing what aliens are like and more about who we are as a species. Wherever, whenever, and whomever the aliens turn out to be, I’m glad that I get to share our little corner of the cosmos with all of you.