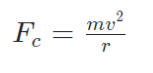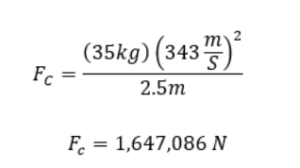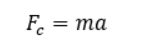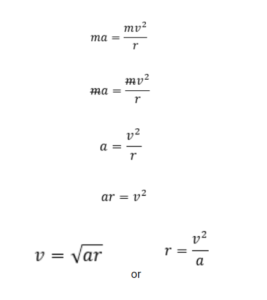I remember the first time I played a Sonic the Hedgehog game. I was 8 years-old and had just bought Sonic Unleashed with my Toys R Us gift card (what a throwback). Coming home, I slapped on the Wii and was thrusted alongside the blue blur himself. As he dashed through levels, I was amazed at his speed and agility, but what really drew my attention was when he ran through one of his signature loops. By all accounts of my 8 year-old logic, that should not have been possible. Sonic should have plummeted straight to the ground at the top of the loop, yet there he was coasting through it.
So what gives? We all know of gravity, the force of attraction, and how Earth’s gravitational pull keeps us on the surface and gives us weight. Why does it seem like Sonic is ignoring gravity through his loops?
The answer to that lies in another force Sonic experiences as he travels through loops, a force called the centripetal force.
How Does Sonic Not Fall Out of a Loop?
Even if you haven’t taken a physics class in a very long time, I’m sure you’ve at least heard of Newton and his iconic three laws of motion, especially the first one about how an object’s direction changes due to forces acting on it. In other words, by Newton’s first law, objects stay moving in one direction until another force acts on them to change their direction, which in technical terms is called inertia. This is what’s happening to Sonic. Sonic enters the loop in a straight path, and as he goes farther into it, his direction begins to change (i.e. he’s moving along the track of the loop now). A force had to have been applied to Sonic to change his direction, this altering force being the normal force. Let’s take a closer look.
Before Sonic dashes into the loop he builds up momentum, which is basically the energy that he’s been accumulating that keeps him moving in the same direction. Thus, as Sonic enters the loop, this momentum stays with him and the inertia causes him to continue forward. However, because the loop is curved, Sonic experiences a change in the direction of the normal force being applied to his feet causing him to also change direction. This normal force is the perpendicular component of the contact force that any object experiences when placed against the surface of another object. No matter where Sonic is in the loop, the normal force will face perpendicular from the track and point towards the center of the loop which leads to the circular path that he follows. This force is the centripetal force, and it allows our blue friend to stay on the track because of the enormous momentum that he built up before entering the loop. From Sonic’s frame of reference, he’s being pushed outwards into the track because it is rising in front of him as he is running causing him to experience what is known as the centrifugal force. But since we are not focusing on Sonic’s frame of reference, rather an outside one viewing him running in the circle, we’ll be referring to this net force causing Sonic to stray from his original path to this circular one as just the previously mentioned centripetal force (Fc).
Centripetal force is generally defined as the force that allows objects to follow curved paths, and it depends on a few things as you can see from the equation above. The mass of the moving object (m), the velocity at which the object moves at the top of the loop (v), and the size of the radius of the circular path that the object is making (r) all play a role in determining how large the centripetal force is. In our case, the moving object of interest is Sonic and the radius of the circular path is the radius of the loop he’s travelling through. Let’s do a simple calculation to see if we can get an idea of the magnitude of centripetal force that might be acting on Sonic during a loop.
Let’s start off with defining the various variables we talked about above. Sonic’s trade calling card is his ability to travel the speed of sound and cause sonic booms, so for velocity (v), we’ll assume Sonic is running at the speed of sound or 343 m/s. For mass (m), this information was a little bit more tricky to find, but after scavenging through a few various video game guides, I found Sonic’s mass to be approximately 35 kg (or 77.1618 pounds). Now onto the radius of the circular path (r). We’ll take a few liberties with deciding the radius of the loops he travels through since they vary heavily from game to game. If we take a look at the original Sonic the Hedgehog game (the image at the very top if you want to follow along!), Sonic’s height is said to be around 100 cm (3’3”ft). If you superpose him multiple times over the loop, the loop appears to be 5 Sonics or 500 cm tall. That means that the radius for this loop would be 250 cm or 2.5 m. If we wanted to get really technical, the radius (r) is from the center of the circular path to the center of mass of the object. Since Sonic isn’t a point mass, we would need to calculate where his center of mass is if we want to be completely accurate. However, since the distance between Sonic’s center of mass and his feet is relatively much smaller than the entire radius of the loop, we will be assuming that Sonic is sufficiently small enough to just be a point mass to make our estimation simpler.
If we take these numbers and plug them into the equation for centripetal force, we get:
Woah! Looks like it’ll take a lot of force for the speedy blue hedgehog to clear this small loop at the speed of sound.
Now, we did the calculations and found a force, but is there a way for us to find the maximum radius of a loop Sonic can travel even if we don’t know the centripetal force? In fact, there is! We’ll just need a little extra help from another concept from our friend Newton.
Gotta Go Fast
We mentioned Newton’s First Law earlier, but now we’re going to need his second one and the very famous equation attached to it: F=ma. This equation simply means that when an object with a mass (m) experiences a net external force acting on it (F), the object will accelerate proportionally to the force applied, where acceleration (a) is just the change in velocity (the direction and speed of the object) over a set time. Let’s look at our case with Sonic. If we say the force applied to him in the loop is the centripetal force, we’ll see a proportional change in Sonic’s acceleration to match. The change in acceleration comes from the change in Sonic’s direction and speed as he’s going around the loop. Therefore, we’ll get this:
So now we have two equations that can describe centripetal force: the one we originally mentioned and now this one from Newton’s Second Law. Since they both describe the same force, we can set them equal to one another and simplify:
As you can see the mass of the object does not matter, as it is cancelled out since it’s on both sides of the equation. We can then rearrange to solve for the radius of the loop in terms of the acceleration on the object and the velocity of the object at the top of the loop. Now, let’s find some values!
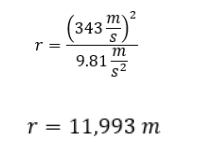Since we (and assuming Sonic) are on Earth, acceleration acting on Sonic is going to be equal to the force of gravity (9.81 m/s2). If we once again say Sonic’s max speed clocks out at the speed of sound (343 m/s), we then have everything we need to solve for the maximum radius of a loop Sonic can travel through!
That means that Sonic can clear a loop that has a radius of 11,993 meters aka one that is 23,986 meters (or 78,694 feet) tall! Insane that this tiny blue hedgehog could do that, right? Remember that the next time you see Sonic clearing a loop in one of his games.
Blue Blur Speeds On
Sonic has always been one of my favorite video game characters and getting to calculate how parts of his game would work in real life is a great way to honor both him and my love for physics. You can do this with anything topic though! I implore you to pick your favorite video game, comic book, or TV character and see if you can use physics or another scientific discipline to better understand how it might be possible for that character to do what they do. Bridge the gap between your interests, and you’ll see just how fun science can be.
Citations
“Sonic the Hedgehog.” Sonic News Network, sonic.fandom.com/wiki/Sonic_the_Hedgehog#Heroes.
“What Is a Centripetal Force? (Article).” Khan Academy, Khan Academy, 2016, www.khanacademy.org/science/physics/centripetal-force-and-gravitation/centripetal-forces/a/what-is-centripetal-force.
“What Is Centripetal Acceleration? (Article).” Khan Academy, Khan Academy, 2016, www.khanacademy.org/science/physics/centripetal-force-and-gravitation/centripetal-acceleration-tutoria/a/what-is-centripetal-acceleration.
